Statistical Framework

We propose a Bayesian statistical framework for real-time inference on the temporal pattern of the reproduction number of an epidemic. Here, the reproduction number R_t for day t will be defined as the mean number of secondary cases infected by a case with symptom onset at day t. Denoting n_t as the number of cases with symptom onset at day t and X_t as the number of secondary cases they infected, the reproduction number R_t is the ratio X_t/n_t, defined for n_t>0.

Assume that we would like to compute the daily values R_t from day 0 to present day T, before the epidemic has ended. Although daily incident case counts can be known up to day T, provided no delay in reporting occurs, the corresponding counts of secondary cases X_t cannot. Secondary case-patients infected before day T, whose illness had a long incubation time, may have clinical onset only after day T. Furthermore, since the exact chain of transmission is seldom observed in practice, attributing secondary cases to previous cases is difficult. Focusing on these 2 issues, we show that the daily counts of symptom onset available until day T are sufficient to estimate R_t.

A 3-step construct is necessary. We first predict the eventual number of late secondary cases (as yet unobserved), for cases reported at day t, assuming the number of early secondary cases (reported before day T) is known. The method described by Wallinga and Teunis (2) is then used to estimate the number of early secondary cases from the daily counts of symptom onsets. These 2 steps are finally combined and yield an estimate of the predictive distribution of R_t. Technical details are given in the Appendix. The estimation procedure depends on 3 assumptions: 1) ascertainment of patients whose symptoms appear before day T is complete, 2) transmission events are independent, and 3) the generation interval, the time from symptom onset in a primary case to symptom onset in a secondary case, has a known frequency distribution.

Data from Hong Kong

The method was retrospectively used to analyze the SARS outbreak in Hong Kong. The data consisted of the dates of symptom onset of the 1,755 case-patients who were detected in Hong Kong in 2003 (4).

Simulated Data

Using simulations, we explored the ability of the method to quickly detect the effect of control measures. Five hundred epidemics were simulated with the following characteristics. During the first 20 days of the epidemics, the theoretical reproduction number was 3. Control measures were implemented at day 20. In a first scenario, control measures were completely effective (no transmission occurred after day 20). In a second scenario, the theoretical reproduction number after control measures were implemented was 0.7. Details on the simulations are available from the corresponding author.

In a simulation study, the bias and precision of the real-time estimator were investigated in situations in which the theoretical reproduction number remained constant with time. We also evaluated the effect of the length of the generation interval on the results. Detailed information can be obtained from the corresponding author.

Application to Hong Kong SARS Data

Figure 1

Figure 1. Application of real-time estimation to the severe acute respiratory syndrome outbreak in Hong Kong. A) Data. B–F) Expectation (solid lines) and 95% credible intervals (dashed lines) of the real-time estimator of...

Figure 1A shows the dates of symptom onset of the 1,755 SARS patients detected in Hong Kong in 2003. Figure 1B–F shows the expectation and 95% credible intervals of the predictive distribution of R_t based on data available at the end of the epidemic and after a lag of 2, 5, 10, and 20 days.

After a lag of 2 days, the 95% credible intervals were wide and displayed an undesirable feature: they sharply decreased to 0 as soon as no cases had been observed for 2 consecutive days (Figure 1C; note especially days 1–4 and 13). After a 5-day lag, this undesirable feature had vanished (Figure 1D).

With lags >5 days, the trends of expected values were relatively similar, with a peak around day 20, a decreasing trend after this date, and the expectation of R_t decreasing to <1 around day 40. These observations suggest that after a lag of only 5 days, the temporal trends in the expectation of R_t are well captured. For a lag of 5 days, the credible interval of R_t was wide when <20 cases were detected (periods 0<t<20 and t>63), but was relatively narrow when more cases were detected (period 21<t<62). As expected, the width of the credible interval narrowed as the lag increased and more complete data were available. The expectations and credible intervals were very similar for lags of 10 and 20 days, 67.8th and 99.7th percentiles, respectively, of the distribution of the SARS generation interval described by Lipsitch et al. (3). No difference was detected between retrospective and 20-day estimates.

Detecting the Effect of Control Measures

Figure 2

Figure 2. Average expectation of the temporal pattern of R_t after implementation of control measures according to the day T of the last observation. A) Completely effective control measures. B) Limited control measures....

In Figure 2, the method is used to estimate the impact of control measures implemented on day 20 in the simulated datasets with completely effective or limited control measures. The curves show the temporal pattern of R_t based on an average over the 500 simulated datasets as a function of T. Even when control measures are completely effective, based on data available up to day 21, the average expectation of R₂₀ is ≈3. Based on data available up to day 25, a downward trend is apparent, whereas based on data available up to day 29, the average expectation of R_t is <1 from t = 27 days. Based on data available up to day 40 (20 days after the implementation of the control measures), the estimates indicate that the threshold value 1 is crossed at day 22, which is 2 days after control measures were implemented. With limited control measures, the observed changes are qualitatively the same, although slightly more time is required for R_t estimates to decrease to <1.

Statistical Framework

Denoting n_t the number of cases with onset at day t and X_t the number of cases they infected, the reproduction number R_t is simply the ratio X_t /n_t defined for n_t>0. Here, we define a method to obtain the predictive distribution of R_t given the available data at day T, where data I(T) = {n_t}_{0< t <T} are the daily counts of incident onsets, assuming that the density w(.) of the generation interval is known. We will make use of the decomposition X_t = X_t^-(T) + X_t⁺(T), where the number of secondary cases X_t from cases with onset at day t has been split in those with onset before T (X_t^-(T)) (early secondary cases), and those with onset after T (X_t⁺(T)) (late secondary cases).

The construction of a global estimator is carried out in 3 stages. First, we consider the problem of right censoring, under the assumption that the exact chain of transmission has been observed until day T. In this situation, X_t^-(T) is observed while X_t⁺(T) is censored and must be predicted, conditional on X_t^-(T) and n_t, to allow computation of the predictive distribution of R_t. Second, when the exact chain of transmission has not been observed, the number of early secondary cases, X_t^-(T), is not available. Following the recommendations of Wallinga and Teunis (1), we show that it is possible to compute the distribution of X_t^-(T) given I(T). Finally, the conditional distributions of X_t⁺(T) given X_t^-(T), n_t and X_t^-(T) given I(T) are combined to derive the distribution of the reproduction number R_t conditional on I(T). All distributions presented are conditional to the number n_t of symptom onsets at day t, but notation is omitted for the sake of clarity.

Distribution of X_t⁺(T) | X_t^-(T)

We assume that X_t is Poisson distributed with mean n_t λ_t and choose a vague gamma prior distribution for λ_t with shape parameter α = 10^-5 and rate β = 10^-5.

Conditional on X_t, the number X_t^-(T) of early secondary cases is binomial with parameters X_t, W_tT, where W_tT is the probability that the generation interval is <T – t. It follows that X_t^-(T) | λ_t is Poisson distributed with mean n_t λ_t W_tT. The same argument would show that X_t⁺(T) | λ_t is Poisson with mean n_t λ_t (1 – W_tT). Given λ_t, X_t⁺(T) and X_t^-(T) are independent so that

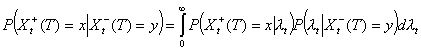
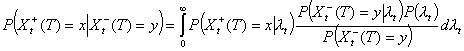
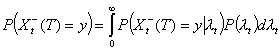
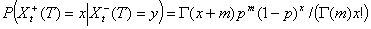
Distribution of X_t^-(T) | I(T)

In practice, the exact realization of X_t^-(T) is unknown, and inference must be based on I(T) alone. Wallinga and Teunis (5) have shown that the probability that a case detected at day k<T has been infected by a case detected at day t<T is

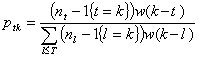
Distribution of R_t | I(T)

Using the decomposition in early and late secondary cases, we obtain

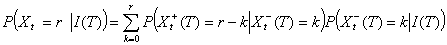
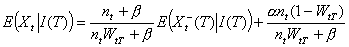
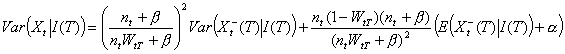
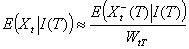
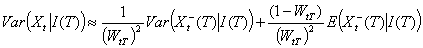
As expected, the average proportion of secondary cases detected before T is W_tT. The first term of the variance is related to our imperfect knowledge of the realization of X_t^-(T) while the second term is related to the natural randomness of X_t⁺(T). We stress that when the lag between day t and day T is large (i.e., W_tT ≈1), our estimates are similar to those of Wallinga and Teunis for complete epidemics.

Given X_t | I(T), the derivation of the predictive distribution of the reproduction number R_t is straightforward considering the deterministic relation R_t = X_t/n_t.