The purpose of this study is to investigate biases inherent in estimating measures of clustering and risk factors for clustering when common sampling strategies are used to collect the empirical data. Since the true distributions of cluster sizes cannot be directly observed if sampling is not complete, I used a Monte Carlo simulation model to generate a variety of hypothetical cluster distributions based on simple assumptions about TB transmission. These distributions represent a wide range of potential data structures reflecting heterogeneous transmission parameters, contact networks, and sociodemographic variables. Accordingly, my aim here is not to model TB transmission dynamics with precision but to generate a collection of heterogeneous cluster distributions that could be used to demonstrate the effects of sampling, given a variety of potential transmission settings.

Generally, the microsimulation model enumerates a population of discrete individuals, each of whom is characterized by a vector of variables that affect risk for TB infection, for clinical disease, and for transmitting infection once infected. Persons are assigned to a series of social and physical spaces such as households, neighborhoods, and multineighborhood communities. The model also specifies the stochastic processes by which latent disease reactivates, infection progresses to primary TB, immunity is conferred by vaccination or by previous infection, and duration of disease is determined. Persons to whom disease is transmitted during the simulation acquire a variable reflecting the strain number of the source of their infection; thus, chains of disease transmission can be identified as “clusters” of cases sharing a specific strain number. The model is run over a time period during which these stochastic processes may occur. Output of the model includes standard measures of the incidence of infection and disease, the prevalence of infectious TB over time, and a count of cluster sizes. Five different cluster distributions were generated on the basis of running the model for 4 years with input variables specific to the different geographic and social settings in which TB is transmitted. The assumptions and baseline input variables for the model have been described (15).

Estimation of Bias in Proportions of Unique and Clustered Cases

The proportion of unique cases calculated after sampling and the variance of that proportion were estimated as follows. Using the “n” method to estimate the proportion of clustered cases, we assume that the true set of isolates is composed of n_k clusters of size k for k = 1,2,…,k_max. Further, we assume that each subject in the true set of isolates is sampled independently with a common sampling probability p.

Let I_ijk be the indicator of whether the i^th subject i =1,...,k from the cluster, j=1,…, n_k, of size k has been sampled. Under our assumptions, the I_ijk are i.i.d. Bernoulli (p) random variables. The total number of subjects sampled is N=. Therefore, the expected value of the number of isolates is

.

The variance of N is var(N) =

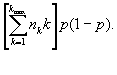
Now let U_jk = 1 if the number of isolates sampled from the j^th cluster of size k is precisely 1 and U_jk = 0 if otherwise. Then the total number of unique isolates is U = . Now U_jk is a Bernoulli random variable with success probability kp(1-p)^k-1 equal to the probability of choosing exactly one member from the j^th cluster of size k. Hence,

var(U) =

The expectation and large sample variance of the random variable (U/N) are derived in Appendix 1. Using these formulae for E(U/N) and var(U/N), estimates of the biased results for a range of sampling fractions were calculated for each of the five transmission scenarios described above. The results of this analysis were verified against a computer simulation that counted cluster sizes after random draws without replacing a proportion p of the true populations of isolates. For each true data set, the simulated data collection process was repeated 1,000 times. The mean value of the estimates obtained is reported, in addition to simulated confidence intervals expressed as values that represented the 0.05th and 0.95th largest estimates. The variance of the empirical distribution for the set of 1,000 simulations was nearly identical to that obtained by the large sample variance formula for a ratio expressed above.

These simulations were repeated using the “n minus one” approach, in which one case per cluster is removed from the count of clustered cases and added to the count of reactivation cases. The analytic solution follows the same logic (Appendix 2).

The recent development of molecular methods to accurately type infectious organisms has led to a marked proliferation in studies of the molecular epidemiology of infectious diseases, especially of TB. The goals of many of these studies have been to address the longstanding problem of assessing the relative proportions of incident TB cases due to recent transmission and to chronic or reactivated disease and to identify risk factors for recent transmission. A systematic bias that consistently underestimates the proportion of cases due to recent transmission could present a serious impediment to the constructive use of molecular typing techniques for studying the epidemiology of infectious disease.

The results of this study show the extent to which bias can be introduced by sampling strategies commonly used in the molecular epidemiology of TB. Depending on the underlying distribution of cluster sizes, the error involved in underestimating the proportion of unique TB isolates in a sample may be sizable, even when up to 70% of the complete data is sampled. The odds ratios for risk factors for clustering are also consistently and markedly underestimated with this approach. The findings of this study support the conclusions of previous investigators (14) who have shown that the extent of error in these estimates is a function of both sampling fraction and underlying cluster distribution in the complete data sets. These results imply that reasonable predictions of the extent of error can be made, given knowledge of both the true distribution of cluster sizes in the population of persons with TB and the size of the population of TB patients from which the sample was drawn. Although the true distribution of cluster sizes cannot be observed in the absence of complete sampling, epidemic models such as this one may elucidate factors that contribute to these distributions and help investigators arrive at prior expectations of cluster distributions in the specific transmission scenarios under study.

I considered how much impact this kind of sampling bias might have had on the studies of the molecular epidemiology of TB published to date. Many researchers report on a convenience sample of cases drawn from one or more clinical sites, without providing an estimate of the number of incident cases in the area in question during the period in which the cases were collected (16–19). In areas with high TB prevalence, the number of cases in these series is often <1% of the number of cases expected in that region on the basis of national reporting or World Health Organization predictions. These results suggest that the bias expected in these studies is so extreme that the findings are useful only as lower bounds for the proportion of recently transmitted cases and for risk factors for recent transmission. Nonetheless, lower bounds may be informative in situations in which undetected transmission is incorrectly attributed to reactivation disease alone or when a new risk factor for transmission is identified.

In industrialized countries with lower rates of incident TB, researchers have tried to enroll a compete cohort of patients by making use of public health reporting systems to identify and fingerprint all new cases of clinical TB in a defined geographic region during a specified time period (4,5,20–22). Although this approach leads to much more complete and systematic sampling, it may not always ensure that the resulting estimates are free from bias. For these series of cases to be complete samples, one would have to assume that none of the cases in the sample had transmission links to cases that did not appear in the study population or were reported before the onset of the study. Furthermore, the most rigorously documented TB fingerprinting studies have reported 15%-40% loss of data as a result of difficulties in culturing, fingerprinting, and interpreting fingerprint patterns (4,5,20–22). Even if the patients excluded from these studies resemble those retained in every other respect, their exclusion will result in a biased outcome of the study.

The “complete” data sets used to estimate bias in this study were generated through stochastic epidemic modeling that outputs cluster distributions in addition to estimates of the incidence of TB infection and disease. Multiple demographic and disease-specific parameters have been found to affect cluster distributions, and many potential “transmission scenarios” could be generated by varying these parameters. In addition, the length of the study period and the stability of the molecular markers used will impact the observed patterns of clustering (23,24). Given that true cluster distributions cannot be known in the absence of complete sampling, the model cannot be validated by using it to derive known cluster distributions. Since the purpose of this study is to explore the bias in measures commonly used in empirical studies of molecular epidemiology, sets of parameters were chosen from a variety of specific areas in which the burden of TB disease has been described or projected based on the information currently available. Although the true transmission patterns in any particular population may be inadequately captured by the epidemic model used, these results do provide some perspective on the potential misinterpretation of molecular data on TB. The simulations may also differ from data sets obtained in the field in that sampling was random and the very real problem of selection bias in the collection of isolates was not addressed. Finally, in the assessment of the bias in the estimates of the effect of risk factors for clustering, I assigned risk status randomly within groups of clustered and unique cases. If cluster size were correlated with a risk factor for clustering, so that, for example, incarceration was more common among cases in large clusters than small ones, the bias in the odds ratio of incarceration would be less than the estimates reported here.

These results demonstrate that estimates of clustering based on molecular fingerprinting of a population of isolates of infectious agents may be severely biased. When these methods are used to estimate the extent of primary and reactivation disease in a community, they consistently underestimate recent transmission. In circumstances in which the error is greatest, the bias may undermine the value of an investigation by providing a community with false reassurance that ongoing transmission is being curtailed and therefore that control measures are adequate.

The findings of this study further suggest that molecular methods in epidemiology require the development of both appropriate epidemiologic study design and analytic tools to yield meaningful assessments of disease transmission. In particular, they imply that estimates of recent transmission obtained by molecular methods cannot be compared across studies which have used different sampling fractions and in which the distribution of cluster size can reasonably be expected to vary. One way for molecular epidemiologists to approach this problem is to provide sensitivity analyses estimating the potential error involved, given prior expectations of cluster distributions and an estimate of the fraction of cases sampled in a particular study. The analytic solution presented here can be easily programmed and used to explore the range of potential error under a variety of hypothetical transmission scenarios.

We wish to derive the expectation and variance of the random variable U/N, denoting the proportion of all sampled isolates that form a unique cluster of size 1 in the sample. In large samples, the mean of U/N is approximately the ratio of the mean of U to the mean of N

E

and the variance of U/N is approximated by the large sample variance formula for a ratio.

var(U/N)

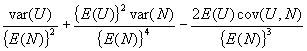
It only remains to evaluate cov(U,N), which is done in the following lemma.

Lemma: Under our assumptions,

cov(U,N) =

Proof: by independence, cov(U,N) = where . Now, cov(U_jk,N_jk) = E(U_jk, N_jk) – E(U_jk)-E(N_jk) = E(U_jk)- E(U_jk)-E(N_jk)= E(U_jk)[1- E(N_jk)] where E(U_jk) = kp(1-p)^{k – 1} and E(N_jk) = n_kp. The result then follows.

The bias in the proportion of reactivated cases after sampling when the clustered cases are counted by using the “n minus one” method is described below. The number of cases considered to be due to reactivation is the sum of the unique cases and the source cases. The “true” number of source cases is equal to the number of clusters in the complete data set, .

We are interested in finding the number of source cases after sampling. Since the number of source cases in a sample is equal to the “true” number of source cases minus the source cases that are not sampled or are sampled as unique, we need to estimate the expected value of the numbers of clusters not sampled and the expected value of the clusters sampled as unique. Let E(CL0) and E(CL1) be the expected values of the numbers of clustered not sampled or sampled as unique, respectively. Then, by using the nomenclature defined in the text and following the logic there described:

E(CL0) = and E(CL1) =

The expected number of source cases after sampling a fraction p of the complete set of isolates is equal to

- -

The overall estimate of the proportion of reactivated cases can then be obtained by summing the number of unique cases after sampling with the number of source cases and dividing by the expected number of sampled isolates, p(N).