Skip directly to site content Skip directly to page options Skip directly to A-Z link Skip directly to A-Z link Skip directly to A-Z link
Volume 8, Number 7—July 2002
Research

Ecologic Niche Modeling and Potential Reservoirs for Chagas Disease, Mexico.

On This Page
Methods
Results
Discussion
Cite This Article
Figures
Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Tables
Table
Downloads
Article
RIS [TXT - 2 KB]
Article Metrics
Metric Details
185
citations of this article
EID Journal Metrics on Scopus
Author affiliations: *Natural History Museum, Lawrence, Kansas, USA; †Universidad Nacional Autónoma de México, D.F., México; ‡Centers for Disease Control and Prevention, Atlanta, Georgia, USA; §and Centro de Investigaciones sobre Enfermedades Infecciosas (CISEI), Cuernavaca, Morelos, México

Cite This Article

Abstract

Ecologic niche modeling may improve our understanding of epidemiologically relevant vector and parasite-reservoir distributions. We used this tool to identify host relationships of Triatoma species implicated in transmission of Chagas disease. Associations have been documented between the protracta complex (Triatoma: Triatominae: Reduviidae) with packrat species (Neotoma spp.), providing an excellent case study for the broader challenge of developing hypotheses of association. Species pairs that were identified coincided exactly with those in previous studies, suggesting that local interactions between Triatoma and Neotoma species and subspecies have implications at a geographic level. Nothing is known about sylvatic associates of T. barberi, which are considered the primary Chagas vector in Mexico; its geographic distribution coincided closely with that of N. mexicana, suggesting interaction. The presence of the species was confirmed in two regions where it had been predicted but not previously collected. This approach may help in identifying Chagas disease risk areas, planning vector-control strategies, and exploring parasite-reservoir associations for other emerging diseases.

Chagas disease is caused by the parasitic protozoan Trypanosoma cruzi and transmitted by blood-feeding insects in the family Reduviidae, subfamily Triatominae. Chagas disease is an important cause of illness and death throughout the Americas, affecting 16–18 million persons. While an estimated 100 million persons in 21 countries in the New World live in endemic areas and are at risk for infection, the disease is principally a zoonotic infection, in which sylvatic mammals serve as reservoir hosts and zoophilic triatomine species as vectors.

The protracta species group consists of seven species (Triatoma protracta, T. peninsularis, T. sinaloensis, T. neotomae, T. barberi, T. nitida, and T. incrassata); T. protracta contains five subspecies: T. p. protracta, T. p. woodi, T. p. navajoensis, T. p. zacatecensis, and T. p. nahuatlae (1,2). This group is restricted to the southwestern United States and Mexico. Previous studies have demonstrated high host specificity in this species group, involving woodrats or packrats (Neotoma spp.) (1). Whereas host associations of Triatoma are often complex, the protracta group shows remarkable host specificity and geographic distributions suggestive of host-ectoparasite cospeciation.

A new tool in the study of geographic phenomena in ecology and systematics is ecologic niche modeling of primary occurrence data (data placing a particular species in a particular state) (3). In general, the approach involves a machine-learning algorithm for discovering associations between point-occurrence data and sets of electronic maps summarizing environmental/ecologic dimensions that may or may not be important in limiting species’ geographic distributions. These associations constitute an approximation of species’ fundamental ecologic niches (the conjunction of ecologic conditions in which a species is able to maintain populations without immigration) (4) and hence provide a basis for understanding numerous ecologic and geographic phenomena related to species distributions.

We applied ecologic niche modeling to identify host relationships of Triatoma species and subspecies implicated in the transmission of Chagas disease. Previous studies by Ryckman (1) provide an ideal test case: hypotheses of association developed based on the modeling approach can be tested independently by using associations identified in Ryckman’s detailed field studies. If successful, this approach would be invaluable in identifying host relationships for species for which detailed information is not available, for stratifying Chagas disease risk areas, and for planning the operational aspects of vector control strategies.

Methods

Point-Occurrence Information

Distribution data for members of the protracta species group were obtained from multiple sources (5–11; state vector control programs in Morelos and San Luis Potosí, unpub. data). Distribution data for Neotoma woodrats occurring in mainland Mexico (excluding offshore islands) were drawn from the Atlas of the Mammals of Mexico (Comisión Nacional para el Conocimiento y Uso de la Biodiversidad, unpub. data) and Hall (12) (textual localities only, georeferenced by hand from 1:50,000-scale maps to approximately 1 km precision). All occurrence data were georeferenced to the nearest 0.001° and organized in Excel 2000 (Microsoft Corp., Redman, WA) spreadsheets for analysis.

Distribution Modeling

Ecologic niches and potential geographic distributions were modeled with the Genetic Algorithm for Rule-Set Prediction (GARP) (13–15), a complex computer application that provides a broader, more objective approach than traditional Geographic Information System (GIS)-based approaches (3) but which yields GIS coverages as output. In general, the procedure focuses on modeling ecologic niches (16). Specifically, GARP relates ecologic characteristics of known occurrence points to those of points randomly sampled from the rest of the study region and develops a series of decision rules that summarizes those factors associated with the species’ presence (3).

All modeling in this study was carried out on a desktop implementation of GARP in a beta-testing stage (R. Scachetti-Pereira, unpub. data). In this software package, occurrence points are divided evenly into training and test data sets. The GARP program works in an iterative process of rule selection, evaluation, testing, and incorporation or rejection: a method is chosen at random from a set of possibilities (e.g., logistic regression, bioclimatic rules), applied to the training data, and a rule is developed (“evolved,” in the terminology of genetic algorithms). At each iteration in the program’s processing, predictive accuracy is then evaluated based on 1,250 points resampled from the test data and 1,250 points randomly sampled from the study region as a whole. Rules may evolve in several ways that genetic algorithms use to mimic DNA evolution (e.g., point mutations, deletions, crossing over). The program uses the change in predictive accuracy from one iteration to the next to evaluate whether a particular rule should be incorporated into the model; the algorithm runs 1,000 iterations or until convergence.

The desktop GARP implementation offers much-improved flexibility (17) in choice of predictive environmental/ecologic GIS data coverage. In this case, we used 11 data layers summarizing elevation; slope; aspect (from the U.S. Geological Survey’s HYDRO 1K data set, http://edcdaac.usgs.gov/gtopo30/hydro/); and aspects of climate, including cloud cover; daily temperature range; mean annual precipitation; maximum, minimum, and mean annual temperatures; vapor pressure; and wind speed (annual means 1960–1990; from the Intergovernmental Panel on Climate Change, http://www.ipcc.ch/). Analysis was limited to Mexico, because of the availability of distribution data for Triatoma, and cell resolution was set at 1x1 km. GARP’s predictive abilities have been tested and proven under diverse circumstances (3,17–23).

To optimize model performance, we developed 100 replicate models of each species’ ecologic niche based on random 50-50 splits of available occurrence points. Unlike previous applications, which either used single models to predict species’ distributions (20) or summed multiple models to incorporate model-to-model variation (19), we used a new procedure (Peterson et al., unpub. data) for choosing best subsets of models. The procedure is based on the observations that 1) models vary in quality, 2) variation in models involves an inverse relationship between errors of omission (leaving out true distribution area) and commission (including areas not actually inhabited), and (3) best models (as judged by experts blinded to error statistics) are clustered in a region of minimum omission of independent test points and moderate area predicted (an axis related directly to commission error). The relative position of the cloud of points relative to the two error axes provides an assessment of the relative accuracy of each model. To choose best subsets of models, we eliminated all models that had nonzero omission error based on independent test points, calculated the average area predicted present in these zero-omission points, and identified models that were within 1% of the overall average. For species or subspecies for which fewer than 10 distribution points were available (which would have a weak extrinsic test of model quality) we developed 20 replicate models based on all points available and summed them as a “best” distribution hypothesis. Five species or subspecies were omitted because of the small sample size (e.g., T. incrassata, with one locality known in Mexico) or distribution outside Mexico (e.g., T. protracta navajoensis), leaving six taxa for analysis: T. p. protracta, T. p. woodi, T. p. zacatecensis, T. peninsularis, T. sinaloensis, and T. barberi.

Projection of the rule-sets for these models onto maps of North America provided distribution predictions. Model quality was tested by the independent sets of points (50%) set aside before GARP modeling: a chi-square test was used to compare observed success in predicting the distribution of test points with that expected under a random model (proportion of area predicted present x number of test points = expected predictive success if points and predictions were random with respect to each other).

Host-Ectoparasite Relationships

The protracta species complex is unusual in that Ryckman studied and documented the ectoparasite-host relationships (1), which provided an independent source of information regarding Triatoma-rodent interactions. In ArcView (version 3.2, ESRI, Redlands, CA), we calculated areas shared between each species or subspecies of the protracta species complex and each species of Neotoma woodrat in Mexico, as well as total modeled distribution areas for each species. We calculated the percent of distribution area (at the highest predicted level in the summed GARP outputs) that each Triatoma species or subspecies shares with each Neotoma species and assumed the most complete overlap values as suggesting an interaction between the species. We then tested these predictions by using the independent information provided by Ryckman (1), asking if species pairs with highest overlap values coincided with interactions identified in Ryckman’s detailed field studies.

Results

Figure 1

Thumbnail of Modeled geographic distributions of Neotoma woodrats in mainland Mexico. (A) black = Neotoma fuscipes, red = N. phenax, green = N. mexicana (note that this distribution includes those of other, less widely distributed, species), yellow = N. goldmani, blue = N. palatina, orange = N. angustapalata. (B) red = N. albigula, yellow = N. micropus, green = N. albigula and N. micropus.

Figure 1. Modeled geographic distributions of Neotoma woodrats in mainland Mexico. (A) black = Neotoma fuscipes, red = N. phenax, green = N. mexicana (note that this distribution includes those of other, less...

Figure 2

Thumbnail of Modeled geographic distributions of members of the protracta species complex: red = Triatoma barberi, yellow = T. p. woodi, green = T. sinaloensis, blue = T. p. protracta, black = T. peninsularis, and pink = T. p. zacatecensis. Only areas predicted for each species at the highest level of confidence (all best-subsets models agree) are shown.

Figure 2. Modeled geographic distributions of members of the protracta species complex: red = Triatoma barberi, yellow = T. p. woodi, green = T. sinaloensis, blue = T. p. protracta, black = T....

Predictions of distributions for all species and subspecies for which >10 points were available were highly statistically significant (all p<0.001) and indeed coincided well with our understanding of known distributions of both insects (JMR and CBB) and woodrats (VSC). For example, T. barberi was predicted to extend broadly across central and southern Mexico, and populations were predicted in several regions (e.g., northern and eastern Michoacán and southern Hidalgo) for which previous occurrence data were not available. After analysis, this species was collected at Tlamaya, Hidalgo (J.C. Noguez-García, pers. comm.), and in northeastern Michoacán (E. Navarro, pers. comm.). Based on the random 50% resampling, in which half the data are set aside to provide an independent test of model quality, the 12 best-subset GARP models for this species were highly statistically significant (average p<10-114). The overprediction of the distribution area for this species in Chiapas represents prediction into areas not inhabited for historical reasons, such as speciation, extinction, or limited dispersal ability (18). Tests for Neotoma species (Figure 1) were also highly significant (N. albigula p<10-18, N. goldmani p<10-16, N. lepida p<10-11, N. mexicana p<10-5, N. micropus p<10-13, and N. phenax p<10-73); some areas of overprediction (e.g., N. mexicana in the Yucatan Peninsula) represent either prediction into areas not inhabited for historic reasons (18) or true overprediction error. Although sufficient point-occurrence data were not available for all species (Figure 2) to permit parallel tests, we are confident in the predictability of our distribution models.

Figure 3

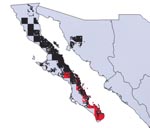
Thumbnail of Modeled geographic distributions of Triatoma peninsularis (red) and Neotoma lepida (black), showing the tight geographic correspondence between the distribution of insect and host mammal. Almost all (93.8%) of the distribution area of T. peninsularis overlaps the distribution area of N. lepida.

Figure 3. Modeled geographic distributions of Triatoma peninsularis (red) and Neotoma lepida (black), showing the tight geographic correspondence between the distribution of insect and host mammal. Almost all (93.8%) of the distribution area...

Figure 4

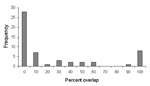
Thumbnail of Frequency distribution of areas of overlap between Triatoma and Neotoma species, expressed as percent of total modeled area (at highest predictive level) of the Triatoma.

Figure 4. Frequency distribution of areas of overlap between Triatoma and Neotoma species, expressed as percent of total modeled area (at highest predictive level) of the Triatoma.

Overlap of areas in Triatoma and Neotoma species and subspecies varied considerably (Table). For example, of the total modeled distribution area of T. peninsularis, 93.8% of the highest confidence prediction coincided with the distribution of N. lepida (Figure 3). Indeed, the overlap values were highly bimodal (Figure 4), suggesting that species’ distributions either coincide or do not overlap, rather than the intermediate peak that might be expected if species did not interact.

The species pairs exhibiting maximum overlap values between Triatoma and Neotoma species (Table) coincided closely with species associations identified by Ryckman (1). Of the six Triatoma analyzed, the maximum overlap values coincided exactly with Ryckman’s identified associations for four of the species. Of the other two species, T. sinaloensis shared 95.5 % of its modeled geographic distribution with N. phenax, an interaction confirmed by Ryckman. However, our model showed no overlap with N. albigula; yet Ryckman found that these two species interacted. Here, the complication is that sample sizes for T. sinaloensis were so small (n = 4) that its distribution was underpredicted. Relaxing the criterion for overlap to include areas predicted present by any of the best-subsets models showed an overlap of 33.2% with N. albigula. The final Triatoma species analyzed, T. barberi, was found by Ryckman (1) exclusively around human domiciles; nevertheless, its geographic distribution coincided closely with that of N. mexicana (98.4% overlap).

Discussion

Ecologic niche modeling and distribution prediction with GARP provides a powerful new tool for applications to disease vectors and reservoirs. Even in systems more poorly understood than that examined here, patterns of overlap in geographic or ecologic space can provide initial hypotheses of host associations and disease reservoir or vector species. In this case, we were able to develop rigorous distribution hypotheses for 15 species of mammals and insects that interact in the potential transmission of Chagas disease in Mexico. These distribution hypotheses can form the basis for many applications in this field, including simple distribution prediction (for example, 3,17,20–22), analysis of specific parameters of species’ ecologic niches (20), prediction of species’ distributions across scenarios of climate change (24,25), prediction of species’ invasions (19), assessment of patterns of evolutionary change in ecologic parameters (18; Martinez-Meyer et al., unpub. data), and spatial/epidemiologic stratification of disease endemic areas.

In general, the species pairs identified by ecologic niche modeling and evaluation of overlap of predicted geographic distributions coincided exactly with the interacting species pairs identified in detailed field studies by Ryckman (1). This result suggests that interactions between Triatoma and Neotoma have implications at a geographic level. That is, a Triatoma species does not simply infest the nests of whichever Neotoma are present at a particular site; rather, geographic distributions of Triatoma species tend to conform closely to those of their Neotoma hosts, suggesting a longer term evolutionary relationship. More detailed ecologic and behavioral studies focused on Triatoma-Neotoma interactions would be invaluable in clarifying the basis for this geographic-scale distribution coincidence.

The only exception to tight coincidence between modeled distribution overlap and Ryckman’s identifications of species interactions was that of T. sinaloensis with N. albigula. This failure is clearly related to the minimal sample size on which the model for T. sinaloensis was based. With increased sample sizes, clearer identification of this interaction should be feasible. Other cases, such as the high overlap of T. p. zacatecensis with Neotoma mexicana and N. micropus (besides the high overlap with its host N. albigula), merit close examination in on-site field studies.

Figure 5

Thumbnail of Modeled geographic distribution of Triatoma barberi, shown with known occurrence points used to create and test the ecologic niche model. Dark red = 100% of best-subsets models predict presence, medium red = 75% of best-subsets models predict presence, light red = 50% of best-subsets models predict presence, lightest red = any best-subsets model predicts presence.

Figure 5. Modeled geographic distribution of Triatoma barberi, shown with known occurrence points used to create and test the ecologic niche model. Dark red = 100% of best-subsets models predict presence, medium red...

The most interesting case is that of T. barberi. Ryckman (1) identified this species as solely associated with human domiciles and did not find it associated with any rodent species. In Oaxaca, this species has been collected in sylvatic habitats near rock outcroppings, but specific host species have not been identified (7). The species’ extensive geographic distribution (Figure 5) coincided closely (98.4% overlap) with that of N. mexicana, at a level that for other Triatoma species would almost certainly indicate an interaction. We suggest two possibilities, which are not mutually exclusive: 1) that T. barberi does indeed parasitize N. mexicana nests, but that additional sampling is necessary to detect this association, or 2) that T. barberi may originally have been an ectoparasite of N. mexicana, but from that host it made the transition to a domestic or peridomestic existence.

Species’ distribution predictions and our capacity to link these distributions with disease transmission are novel epidemiologic tools. Understanding sylvatic transmission cycles and invasion of peridomestic habitats is an immediate application for niche analysis and modeling. This general approach has potential applications much broader than the protracta species complex and Neotoma associations as they relate to Chagas disease transmission. We anticipate addressing host relationships in other Triatoma such as the phyllosoma group, the most important complex of vector species of Chagas disease in Mexico and for which host relationships are all but unknown (7). Sylvatic reservoir species for many tropical diseases remain poorly documented (e.g., leishmaniasis, hantavirus pulmonary syndrome, West Nile encephalitis, leptospirosis) and our approach provides a strategy for narrowing the field of possible species and ecologic scenarios.

Dr. Peterson is associate professor of ecology and evolutionary biology and curator of ornithology in the Natural History Museum and Biodiversity Research Center, University of Kansas. His research interests focus on understanding factors affecting species’ geographic distributions, including aspects of evolution, phylogenetics, and geography.

Top

Acknowledgments

Many thanks to Ricardo Scachetti-Pereira for developing the desktop version of GARP and to David Vieglais for myriad developments in the emerging field of biodiversity informatics.

This research was supported by grants from the National Science Foundation; VSC was supported by the Dirección General de Asuntos del Personal Académico, Universidad Nacional Autónoma de México; JMR was supported by the European Community Latin American Network (ECLAT) and Instituto Nacional de Salud Pública, Mexico.

Top

References

  1. Ryckman  RE. Biosystematics and hosts of the Triatoma protracta complex in North America (Hemiptera: Reduviidae) (Rodentia: Cricetidae). University of California Publications in Entomology. 1962;27:93–240.
  2. Lent  H, Wygodzinsky  P. Revision of the Triatominae (Hemiptera: Reduviidae) and their significance as vectors of Chagas disease. Bull Am Mus Nat Hist. 1979;163:125–520.
  3. Peterson  AT, Stockwell  DRB, Kluza  DA. Distribution prediction based on ecologic niche modeling of primary occurrence data. In: Scott JM, editor. Predicting species occurrences: issues of scale and accuracy. Washington: Island Press; 2001.
  4. MacArthur  RH. Geographical ecology. Princeton (NJ): Princeton University Press; 1972.
  5. Gomez-Torres  R, Rodríguez-Vázquez  ML, Mooser-Barandum  O, Ramirez-Isunza  JM. Enfermedad de Chagas en el estado de Aguascalientes. Arch Inst Cardiol Mex. 1983;53:139–42.PubMedGoogle Scholar
  6. Magallon-Gastélum  E, Magdaleno-Peñaloza  NC, Katthain-Duchateau  G, Trujillo-Contreras  F, Lozano-Kasten  FJ, Hernández-Gutiérrez  RJ. Distribución de los vectores de la enfermedad de Chagas (Hemiptera: Reduviidae: Triatominae), en el estado de Jalisco, México. Revista Biomedica. 1998;9:151–7.
  7. Ramsey  J, Ordoñez  R, Cruz-Celis  A, Alvear  A, Chavez  V, Lopez  R, Distribution of domestic Triatominae and stratification of Chagas disease transmission in Oaxaca, México. Med Vet Entomol. 2000;14:19–30. DOIPubMedGoogle Scholar
  8. Rojas  JC, Malo  EA, Espinoza-Medinilla  E, Ondarza  RN. Sylvatic focus of Chagas disease in Oaxaca, Mexico. Ann Trop Med Parasitol. 1989;83:115–20.PubMedGoogle Scholar
  9. Tay  J. La enfermedad de Chagas en la República Mexicana. Revista Salud Pública de Mexico. 1980;22:409–50.
  10. Zarate  LG, Zarate  RJ. A checklist of the Triatominae (Hemiptera: Reduvidae) of Mexico. International Journal of Entomology. 1985;27:102–27.
  11. Vidal-Acosta  V, Ibañez-Bernal  S, Martínez-Campos  C. Infección natural de chinches Triatominae con Trypanosoma cruzi asociadas a la vivienda humana en México. Salud Publica Mex. 2000;42:496–503. DOIPubMedGoogle Scholar
  12. Hall  ER. The mammals of North America, vol. 2. New York: Wiley & Sons; 1981.
  13. Stockwell  DRB. Genetic algorithms II. In: Fielding AH, editor. Machine learning methods for ecologic applications. Boston: Kluwer Academic Publishers; 1999. p. 123–44.
  14. Stockwell  DRB, Noble  IR. Induction of sets of rules from animal distribution data: a robust and informative method of analysis. Math Comput Simul. 1992;33:385–90. DOIGoogle Scholar
  15. Stockwell  DRB, Peters  DP. The GARP modelling system: problems and solutions to automated spatial prediction. Int J Geogr Inf Sci. 1999;13:143–58. DOIGoogle Scholar
  16. Grinnell  J. Field tests of theories concerning distribution control. Am Nat. 1917;51:115–28. DOIGoogle Scholar
  17. Peterson  AT, Cohoon  KC. Sensitivity of distribution prediction algorithms to geographic data completeness. Ecol Modell. 1999;117:159–64. DOIGoogle Scholar
  18. Peterson  AT, Soberon  J, Sánchez-Cordero  V. Conservatism of ecologic niches in evolutionary time. Science. 1999;285:1265–7. DOIPubMedGoogle Scholar
  19. Peterson  AT, Vieglais  DA. Predicting species invasions using ecologic niche modeling. Bioscience. 2001;51:363–71. DOIGoogle Scholar
  20. Peterson  AT. Predicting species’ distributions based on ecologic niche modeling. Condor. 2001;103:599–605. DOIGoogle Scholar
  21. Peterson  AT, Ball  LG, Cohoon  KC. Predicting distributions of tropical birds. Ibis. 2002. In press.
  22. Stockwell  DRB, Peterson  AT. Controlling bias in biodiversity data. In: Scott JM, editor. Predicting species occurrences: issues of scale and accuracy. Washington: Island Press. In press 2001.
  23. Feria  ATP, Peterson  AT. Prediction of bird community composition based on point-occurrence data and inferential algorithms: a valuable tool in biodiversity assessments. Divers Distrib. 2002;8:49–56. DOIGoogle Scholar
  24. Peterson  AT, Sánchez-Cordero  V, Soberón  J, Bartley  J, Buddemeier  RW, Navarro-Sigüenza  AG. Effects of global climate change on geographic distributions of Mexican Cracidae. Ecol Modell. 2001;144:21–30. DOIGoogle Scholar
  25. Peterson  AT, Ortega-Huerta  M, Bartley  J, Sánchez-Cordero  V, Soberón  J, Buddemeier  RH, Biodiversity consequences of global climate change in Mexico. Nature. 2002. In press.PubMedGoogle Scholar

Top

Figures
Table

Top

Cite This Article

DOI: 10.3201/eid0807.010454

Table of Contents – Volume 8, Number 7—July 2002

EID Search Options
presentation_01 Advanced Article Search – Search articles by author and/or keyword.
presentation_01 Articles by Country Search – Search articles by the topic country.
presentation_01 Article Type Search – Search articles by article type and issue.

Top

Comments

Please use the form below to submit correspondence to the authors or contact them at the following address:

A. Townsend Peterson, Natural History Museum, University of Kansas, Lawrence, Kansas 66045, USA; fax: 785-864-5335;

Send To

10000 character(s) remaining.

Top

Page created: July 16, 2010
Page updated: July 16, 2010
Page reviewed: July 16, 2010
The conclusions, findings, and opinions expressed by authors contributing to this journal do not necessarily reflect the official position of the U.S. Department of Health and Human Services, the Public Health Service, the Centers for Disease Control and Prevention, or the authors' affiliated institutions. Use of trade names is for identification only and does not imply endorsement by any of the groups named above.
file_external