Skip directly to site content Skip directly to page options Skip directly to A-Z link Skip directly to A-Z link Skip directly to A-Z link
CDC’s website is being modified to comply with President Trump’s Executive Orders.
Volume 11, Number 8—August 2005
Research

Optimizing Treatment of Antimicrobial-resistant Neisseria gonorrhoeae

Kakoli Roy*Comments to Author , Susan A. Wang*, and Martin I. Meltzer*
Author affiliations: *Centers for Disease Control and Prevention, Atlanta, Georgia, USA

Main Article

Figure 1

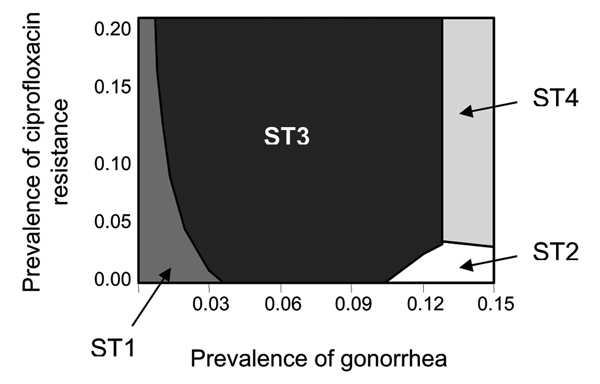
Lowest cost per patient successfully treated on varying prevalence of gonorrhea and prevalence of ciprofloxacin-resistant Neisseria gonorrhoeae. Notes: strategy depicted is optimal (lowest cost per patient successfully treated) for given combinations of prevalence of gonorrhea and prevalence of ciprofloxacin-resistant N. gonorrhoeae. Since the alternative strategies are similar in effectiveness, cost-effectiveness analysis does not offer a practical decision-making tool. Instead, cost minimizati

Figure 1. . Lowest cost per patient successfully treated on varying prevalence of gonorrhea and prevalence of ciprofloxacin-resistant Neisseria gonorrhoeae. Notes: strategy depicted is optimal (lowest cost per patient successfully treated) for given combinations of prevalence of gonorrhea and prevalence of ciprofloxacin-resistant N. gonorrhoeae. Since the alternative strategies are similar in effectiveness, cost-effectiveness analysis does not offer a practical decision-making tool. Instead, cost minimization, which selects as optimal a strategy that costs least while achieving the same level of effectiveness (i.e., per case of successful treatment), serves as a more practical and intuitive tool kit for decision making. Case-patients refer to all women who attend a public health clinic and undergo therapy as per 1 of the 4 strategies, regardless of actual infection. The strategies modeled were ST1: ciprofloxacin + culture-based tests + ciprofloxacin-susceptibility tests; ST2: ciprofloxacin + nonculture-based tests; ST3: ceftriaxone + culture-based tests + ceftriaxone-susceptibility tests; ST4: ceftriaxone + nonculture-based tests (see Table 1 and text for further details). Values for input variables other than prevalence of gonorrhea and prevalence of ciprofloxacin-resistant N. gonorrhoeae are the base case values given in Tables 2 and 3.

Main Article

1In 2000, only 18% of gonorrhea tests performed by public health laboratories in the United States were culture-based tests.

2Monte Carlo simulation involves specifying a probability distribution of values for model inputs. A computer algorithm then runs the model for several iterations. During each iteration, the computer algorithm selects input values from the probability distributions, and calculates the output (e.g., cost per patient successfully treated). After the final run, the model provides results such as the mean, median, and 5th and 95th percentiles for each specified output.

Page created: April 23, 2012
Page updated: April 23, 2012
Page reviewed: April 23, 2012
The conclusions, findings, and opinions expressed by authors contributing to this journal do not necessarily reflect the official position of the U.S. Department of Health and Human Services, the Public Health Service, the Centers for Disease Control and Prevention, or the authors' affiliated institutions. Use of trade names is for identification only and does not imply endorsement by any of the groups named above.
file_external