Volume 7, Number 3—June 2001
Synopsis
Spoligotype Database of Mycobacterium tuberculosis: Biogeographic Distribution of Shared Types and Epidemiologic and Phylogenetic Perspectives
Table 2
Geographic distribution of potentially specific shared types of Mycobacterium tuberculosis reported in a single location (n=122)
| Region | Country | No. of types | Types |
|---|---|---|---|
| Americas | Guadeloupe | 7 | 12,13,14,15,30,103,259 |
| French Guiana | 4 | 66,76,94,96 | |
| Cuba | 4 | 71,74,80,81 | |
| USA | 46 | 192,194,197-199,201,202, 205,206,208,210-217,219-235, 237-239,241,243,246,248,256-258 | |
| Europe | The Netherlands | 4 | 9,18,28,90 |
| United Kingdom | 6 | 16,23,27,38,43,100 | |
| France | 27 | 55,57,107-114,116,120,122, 140,141,143-148,170,171, 173,174,184,186 | |
| Italy | 9 | 155,157-160,163,165,166,169 | |
| Spain | 2 | 104,106 | |
| Russia | 3 | 251,252,253 | |
| Africa | Zimbabwe | 6 | 79,82-85,87 |
| Guinea-Bissau | 1 | 188 | |
| Asia | Philippines | 1 | 69 |
| Mongolia | 2 | 97, 98 |
1For this purpose, the independent sampling sizes for Europe and the USA were taken as n1 and n2, the number of individuals within a given shared-type "x" was k1 and k2, and in this case, the representativeness of the two samples was p1=k1/n1 and P2=k2/n2, respectively. To assess if the divergence observed between p1 and p2 was due to sampling bias or the existence of two distinct populations, the percentage of individuals (p0) harboring shared-type "x" in the population studied was estimated by the equation p0= k1+k2/n1+n2=n1p1+n2p2/n1+n2. The distribution of the percentage of shared-type "x" in the sample sizes n1 and n2 follows a normal distribution with a mean p0 and a standard deviation of 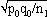 and
and 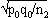 respectively, and the difference d=p1-p2 follows a normal distribution of mean p0-p0=0 and of variance σd2=σp12+σp22 = p0q0/n1+p0q0/n2 or σd2=p0q0 (1/n1+1/n2). The two samples being independent, the two variances were additive; the standard deviation σd=
respectively, and the difference d=p1-p2 follows a normal distribution of mean p0-p0=0 and of variance σd2=σp12+σp22 = p0q0/n1+p0q0/n2 or σd2=p0q0 (1/n1+1/n2). The two samples being independent, the two variances were additive; the standard deviation σd=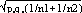 . If the absolute value of the quotient d/σd<2, the two samples were considered to belong to a same population (CI 95%) and the variation observed in the distribution of isolates for given shared types could be due to a sampling bias. Inversely, if d/σd>2, then the differences observed in the distribution of isolates for given shared types were statistically significant and not due to potential sample bias.
. If the absolute value of the quotient d/σd<2, the two samples were considered to belong to a same population (CI 95%) and the variation observed in the distribution of isolates for given shared types could be due to a sampling bias. Inversely, if d/σd>2, then the differences observed in the distribution of isolates for given shared types were statistically significant and not due to potential sample bias.