Volume 7, Number 3—June 2001
Synopsis
Spoligotype Database of Mycobacterium tuberculosis: Biogeographic Distribution of Shared Types and Epidemiologic and Phylogenetic Perspectives
, Ingrid Filliol*, Maria Cristina Gutierrez†, Igor Mokrousov*, Véronique Vincent†, and Nalin Rastogi*
Table 4
Analysis of distribution of shared types found in both USA and Europea
| Europe |
USA |
World |
|||||
|---|---|---|---|---|---|---|---|
| No. |
%b |
No. |
% |
% |
d/σd | ||
| Type | (k1) | (p1) | (k2) | (p2) | No. | (p0) | quotientc |
| 1 | 21 | 1.8 | 326 | 25.5 | 476 | 14.4 | 15.3d |
| 2 | 6 | 0.5 | 2 | 0.2 | 28 | 0.8 | 1.6 |
| 8 | 10 | 0.9 | 7 | 0.5 | 19 | 0.6 | 0.9 |
| 19 | 1 | 0.1 | 23 | 1.8 | 27 | 0.8 | 4.2d |
| 20 | 8 | 0.7 | 2 | 0.2 | 20 | 0.6 | 2.1d |
| 25 | 13 | 1.1 | 3 | 0.2 | 17 | 0.5 | 2.7d |
| 26 | 22 | 1.9 | 5 | 0.4 | 28 | 0.8 | 3.6d |
| 33 | 13 | 1.1 | 10 | 0.8 | 38 | 1.2 | 0.9 |
| 34 | 6 | 0.5 | 9 | 0.7 | 21 | 0.6 | 0.6 |
| 37 | 17 | 1.5 | 2 | 0.2 | 28 | 0.8 | 3.7d |
| 44 | 12 | 1.1 | 1 | 0.1 | 15 | 0.5 | 3.3d |
| 47 | 25 | 2.2 | 23 | 1.8 | 65 | 2.0 | 0.7 |
| 48 | 34 | 3.0 | 7 | 0.5 | 41 | 1.2 | 4.6d |
| 50 | 56 | 4.9 | 32 | 2.5 | 155 | 4.7 | 3.1d |
| 52 | 29 | 2.5 | 7 | 0.5 | 40 | 1.2 | 4.0d |
| 53 | 79 | 6.9 | 46 | 3.6 | 218 | 6.6 | 3.6d |
| 58 | 4 | 0.4 | 7 | 0.5 | 17 | 0.5 | 0.7 |
| 62 | 7 | 0.6 | 4 | 0.3 | 15 | 0.5 | 1.1 |
| 92 | 2 | 0.2 | 8 | 0.6 | 14 | 0.4 | 1.7 |
| 118 | 8 | 0.7 | 1 | 0.1 | 9 | 0.3 | 2.5d |
| 119 | 2 | 0.2 | 110 | 8.6 | 115 | 3.5 | 9.6d |
| 137 | 10 | 0.9 | 134 | 10.5 | 146 | 4.4 | 9.7d |
| 138 | 5 | 1 | 1 | 0.1 | 6 | 0.2 | 1.8 |
| 139 | 19 | 1.7 | 19 | 1.5 | 38 | 1.2 | 0.3 |
aResults are given for 24 of 45 shared types that contained enough isolates to compare the results statistically.
bPercentages were calculated on the basis of 1,142 (n1), 1,276 (n2), and 3,319 individual spoligotypes reported, respectively, for Europe (p1), USA (p2), and the full database available for the world.
cThe quotient d/σd was calculated by using the equation d/σd=p1-p2/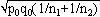 
, where d is the absolute value of the difference between p1 and p2, σd is the standard deviation of the repartition law of d which follows a normal distribution and can be calculated by the equation σd =
dIf the absolute value of the quotient d /σd<2, the variations observed in the distribution of isolates for a given shared type were not statistically significant and could be due to a sampling bias. Inversely, if d /σd>2, then the differences observed in the distribution of isolates for a given shared type were statistically significant and not due to a potential sample bias.
1For this purpose, the independent sampling sizes for Europe and the USA were taken as n1 and n2, the number of individuals within a given shared-type "x" was k1 and k2, and in this case, the representativeness of the two samples was p1=k1/n1 and P2=k2/n2, respectively. To assess if the divergence observed between p1 and p2 was due to sampling bias or the existence of two distinct populations, the percentage of individuals (p0) harboring shared-type "x" in the population studied was estimated by the equation p0= k1+k2/n1+n2=n1p1+n2p2/n1+n2. The distribution of the percentage of shared-type "x" in the sample sizes n1 and n2 follows a normal distribution with a mean p0 and a standard deviation of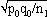 
and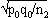 
respectively, and the difference d=p1-p2 follows a normal distribution of mean p0-p0=0 and of variance σd2=σp12+σp22 = p0q0/n1+p0q0/n2 or σd2=p0q0 (1/n1+1/n2). The two samples being independent, the two variances were additive; the standard deviation σd=
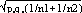. If the absolute value of the quotient d/σd<2, the two samples were considered to belong to a same population (CI 95%) and the variation observed in the distribution of isolates for given shared types could be due to a sampling bias. Inversely, if d/σd>2, then the differences observed in the distribution of isolates for given shared types were statistically significant and not due to potential sample bias.